路边工程院数学&物理部物理公式

近似方法, 量子力学

2025-07-23

微扰论

文章目录

1. 定态微扰论
1. 1.1. 非简并态微扰
  1. 1.1.1. 一阶近似
  2. 1.1.2. 二阶近似
2. 1.2. 简并态微扰
  1. 1.2.1. 一阶近似
  2. 1.2.2. 二阶近似
2. 含时微扰论

定态微扰论

非简并态微扰

定态微扰论 (Stationary Perturbation Theory) 的前提为扰动是与时间无关的, 并且是微小的. 利用该理论可以通过在已知无微扰下的精确解来获得存在微扰时的体系近似解. 存在微扰时的系统哈密顿量可以分解为两项

$H=H_0 + \lambda H^{'}$

其中 $H^{'}$ 为微扰项, 并且使用一个很小的实参数 $\lambda$ 来反映其微小程度. 然后将 $\psi _n$ 与 $E_n$ 展开为 $\lambda$ 的幂级数:

$\psi _n=\psi _n ^{(0)}+\lambda \psi _n ^{(1)} +\lambda ^2 \psi _n ^{(2)} + ...$

$E_n = E_n^{(0)}+\lambda E_n^{(1)}+\lambda ^2 E_n^{(2)} + ...$

其中 $E_n^{(0)}$ , $\psi _n ^{(0)}$ 为无微扰下 $H_0$ 的第 $n$ 个本征值的精确解, $E_n^{(1)}$ , $\psi _n ^{(1)}$ 为第 $n$ 个本征值的一阶修正 (first-order correction) , $E_n^{(2)}$ , $\psi _n ^{(2)}$ 为二阶修正 (second-order correction) , 之后的依此类推. 将上述二式代入定态薛定谔方程可得

$(H_0 + \lambda H^{'})(\psi _n ^{(0)}+\lambda \psi _n ^{(1)} +\lambda ^2 \psi _n ^{(2)} + ...)=(E_n^{(0)}+\lambda E_n^{(1)}+\lambda ^2 E_n^{(2)})(\psi _n ^{(0)}+\lambda \psi _n ^{(1)} +\lambda ^2 \psi _n ^{(2)} + ...)$

并将 $\lambda$ 的相同幂次项合并:

$H_0 \psi _n ^{(0)} + \lambda (H_0 \psi _n ^{(1)} + H^{'}\psi _n ^{(0)}) + \lambda ^2 (H_0 \psi _n ^{(2)} + H^{'} \psi _n ^{(1)})+ ... =E_n^{(0)} \psi _n ^{(0)} + \lambda (E_n^{(0)} \psi _n ^{(1)} + E_n^{(1)} \psi _n ^{(0)}) + \lambda ^2 (E_n^{(0)} \psi _n ^{(2)} + E_n^{(1)} \psi _n ^{(1)} + E_n^{(2)} \psi _n ^{(0)} )$

对于零阶 ( $\lambda ^0$ )有 $H_0 \psi _n ^{(0)} =E_n^{(0)} \psi _n ^{(0)}$ , 显然这是无微扰时的状态, 并且是可以精确求解的.

对于一阶 ( $\lambda ^1$ )有

$H_0 \psi _n ^{(1)} + H^{'}\psi _n ^{(0)}=E_n^{(0)} \psi _n ^{(1)} + E_n^{(1)} \psi _n ^{(0)}$

对于二阶 ( $\lambda ^1$ ) 有

$H_0 \psi _n ^{(2)} + H^{'} \psi _n ^{(1)}=E_n^{(0)} \psi _n ^{(2)} + E_n^{(1)} \psi _n ^{(1)} + E_n^{(2)} \psi _n ^{(0)}$

一阶近似

现在讨论一阶的情况, 为得到一阶的能量修正 , 使用 $\psi _n^{(0)}$ 对于一阶的情况进行内积运算, 可得

$\langle \psi _n^{(0)} | H_0 \psi _n ^{(1)} \rangle + \langle \psi _n^{(0)} | H^{'}\psi _n ^{(0)} \rangle = \langle \psi _n^{(0)} | E_n^{(0)} \psi _n ^{(1)} \rangle + \langle \psi _n^{(0)} | E_n^{(1)} \psi _n ^{(0)} \rangle$

即

$E_n^{(0)} \langle \psi _n^{(0)} | \psi _n ^{(1)} \rangle + \langle \psi _n^{(0)} | H^{'} | \psi _n ^{(0)} \rangle = E_n^{(0)} \langle \psi _n^{(0)} | \psi _n ^{(1)} \rangle + E_n^{(1)} \langle \psi _n^{(0)} | \psi _n ^{(0)} \rangle$

于是左右两边第一项相消, 右式第二项由本征矢的正交归一性等于 $E_n^{(1)}$ .即:

$E_n^{(1)}=\langle \psi _n^{(0)} | H^{'} | \psi _n ^{(0)} \rangle$

上式即为能量的一阶修正, 也就是 $H^{'}$ 在 $H_0$ 表象下的矩阵元. 现在继续求波函数的一级修正, 将一阶情况改写为合并了波函数的形式:

$(H_0 - E_n^{(0)}) \psi _n ^{(1)} = - (H^{'}-E_n^{(1)})\psi _n ^{(0)}$

将 $\psi _n ^{(1)}$ 使用未微扰的本征函数完备系进行展开:

$\psi _n ^{(1)}=\sum _{m \ne n} c_m \psi _m ^{(0)}$

于是现在的问题变为解决系数 $c_m$ 的问题, 现将上式带回刚刚改写的合并波函数的式子(求和中去掉 $\psi _n ^{(0)}$ 这一项的原因是如果 $\psi _n ^{(1)}$ 满足一级情况, 那么对于任意常数 $\alpha$ , $(\psi _n ^{(1)} + \alpha \psi _n ^{(0)})$ 亦满足一级情况, 因此无需对 $\psi _n ^{(0)}$ 也求和了), 可得:

$\sum _{m \ne n}(E_m^{(0)}-E_n^{(0)})c_m \psi _m ^{(0)}=- (H^{'}-E_n^{(1)})\psi _n ^{(0)}$

现取本征函数系中的一 $l \ne n$ 的波函数 $\psi _l^{(0)}$ 与上式进行内积, 得到:

$\sum _{m \ne n}(E_m^{(0)}-E_n^{(0)})c_m \langle \psi _l^{(0)} | \psi _m ^{(0)} \rangle =- \langle \psi _l^{(0)} |H^{'}|\psi _n ^{(0)} \rangle + E_n^{(1)}) \langle \psi _l^{(0)} |\psi _n ^{(0)} \rangle$

又由于 $l \ne n$ , 于是由正交归一性得:

$(E_l^{(0)}-E_n^{(0)})c_l= -\langle \psi _l^{(0)} |H^{'}|\psi _n ^{(0)} \rangle$

于是可得:

$c_m=\frac{\langle \psi _m^{(0)} |H^{'}|\psi _n ^{(0)} \rangle}{E_n^{(0)}-E_m^{(0)}}$

则波函数的一级修正为:

$\psi _n ^{(1)}=\sum _{m \ne n} \frac{\langle \psi _m^{(0)} |H^{'}|\psi _n ^{(0)} \rangle}{E_n^{(0)}-E_m^{(0)}} \psi _m ^{(0)}$

二阶近似

现在把二阶情况再写一遍:

$H_0 \psi _n ^{(2)} + H^{'} \psi _n ^{(1)}=E_n^{(0)} \psi _n ^{(2)} + E_n^{(1)} \psi _n ^{(1)} + E_n^{(2)} \psi _n ^{(0)}$

对于二阶情况的能量修正, 同对一阶情况的处理一样, 将 $\psi _n^{(0)}$ 与上式进行内积, 得到

$\langle \psi _n^{(0)} |H_0 \psi _n ^{(2)} \rangle +\langle \psi _n^{(0)} | H^{'} \psi _n ^{(1)} \rangle =E_n^{(0)} \langle \psi _n^{(0)} |\psi _n ^{(2)} \rangle + E_n^{(1)} \langle \psi _n^{(0)} |\psi _n ^{(1)} \rangle + E_n^{(2)} \langle \psi _n^{(0)} | \psi _n ^{(0)} \rangle$

同理左式第一项与右式第一项消掉, 再由正交归一性得:

$E_n^{(2)} = \langle \psi _n^{(0)} | H^{'} \psi _n ^{(1)} \rangle -E_n^{(1)} \langle \psi _n^{(0)} |\psi _n ^{(1)} \rangle$

又由于 $\psi _n ^{(1)}=\sum _{m \ne n} c_m \psi _m ^{(0)}$ ,则有:

$\langle \psi _n^{(0)} |\psi _n ^{(1)} \rangle=\sum _{m \ne n} c_m \langle \psi _n^{(0)} |\psi _m ^{(0)} \rangle =0$

即:

$E_n^{(2)} = \langle \psi _n^{(0)} | H^{'} \psi _n ^{(1)} \rangle=\sum _{m \ne n} c_m \langle \psi _n^{(0)} | H^{'} |\psi _m ^{(0)} \rangle = \sum _{m \ne n} \frac{| \langle \psi _m^{(0)} |H^{'}|\psi _n ^{(0)} \rangle |^2}{E_n^{(0)}-E_m^{(0)}}$

即能量的二阶修正为:

$E_n^{(2)} = \sum _{m \ne n} \frac{| \langle \psi _m^{(0)} |H^{'}|\psi _n ^{(0)} \rangle |^2}{E_n^{(0)}-E_m^{(0)}}$

即二级修正依赖于 $H_0$ 的除 $\psi _n^{(0)}$ 以外全部波函数, 可采用下图进行理解

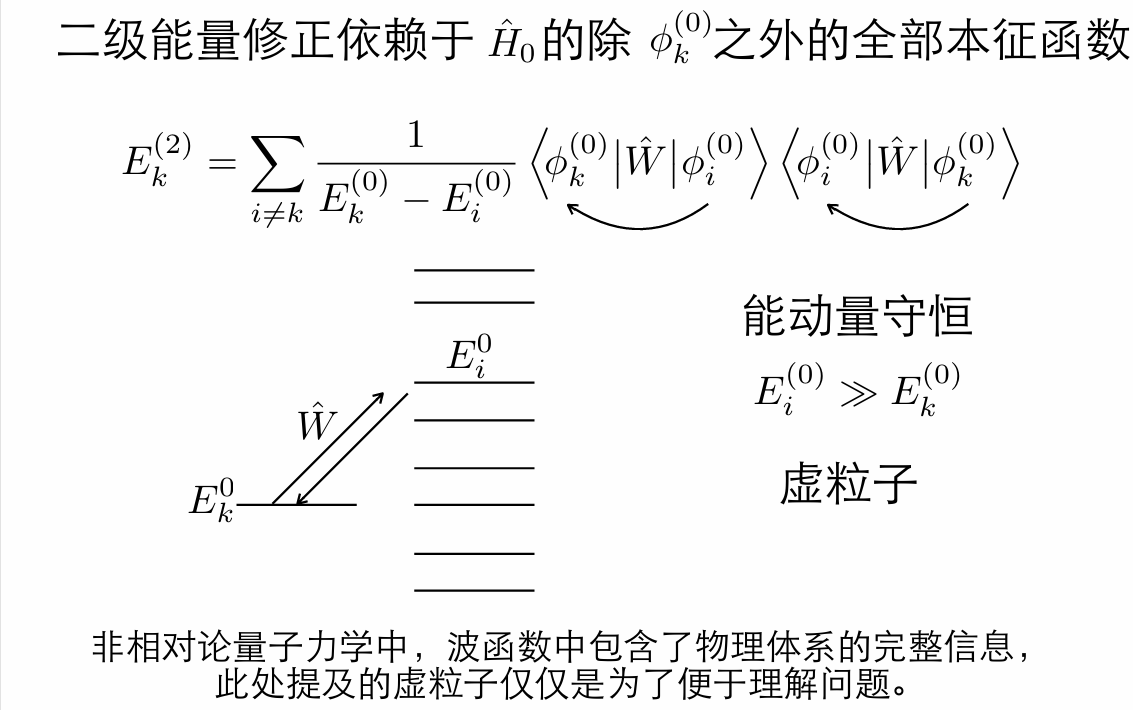
微扰论2

同理可以利用微扰论继续计算波函数的二阶修正, 能量的三阶修正…等, 这里就不做推导了. Griffiths 书上有写 Landau 的那本量子力学有讲更高阶的修正与推导高阶修正公式的一般方法, 不过我没看过那本, 这里就不写了, 也许以后会写, 这里仅给出能量的三阶修正表达式:

$E_n^{(3)}=\sum _{m,m^{'} \ne n}\frac{H_{nm}^{'}H_{mm^{'}}^{'}H_{m^{'}n}^{'}}{(E_n^{(0)}-E_m^{(0)})(E_n^{(0)}-E_{m^{'}}^{(0)})}- \sum _{m \ne n}\frac{H_{nn}^{'}|H_{mn}^{'}|^2}{(E_n^{(0)}-E_m^{(0)})^2}$

简并态微扰

如果未微扰时的本征矢存在简并, 那么显然非简并态下的微扰论将不再使用(一个显然的例子是对于能量二级修正将使得分母为0,使得结果发散). 接下来讨论简并态微扰 (Degenerate Perturbation Theory) 的情况.

以二重简并为例(更多重简并也同理, 仅仅是矩阵阶数的差异而已), 假设 $\psi _a^{(0)}$ 与 $\psi _n^{(0)}$ 是简并的, 即

$H_0 \psi _a^{(0)} =E^{(0)} \psi _a^{(0)} \qquad H_0 \psi _b^{(0)} =E^{(0)} \psi _b^{(0)} \qquad \langle \psi _a^{(0)} | \psi _b^{(0)} \rangle =0$

那么 $\psi _a^{(0)}$ 与 $\psi _n^{(0)}$ 的线性组合显然也是 $H_0$ 的本征态, 并且本征值也为 $E$ :

$\psi ^{(0)}=\alpha \psi _a^{(0)}+\beta \psi _b^{(0)} \qquad H_0 \psi ^{(0)} =E^{(0)} \psi ^{(0)}$

通常微扰 $H^{'}$ 会消除这一简并, 使得 $\psi _a^{(0)}$ 与 $\psi _n^{(0)}$ 退简并, 将原来无微扰的能级 $E^{(0)}$ 分裂成两个能级. 于是现在的问题变成了如何求解 “好” 的 $\psi _a^{(0)}$ 与 $\psi _n^{(0)}$ 的线性组合.

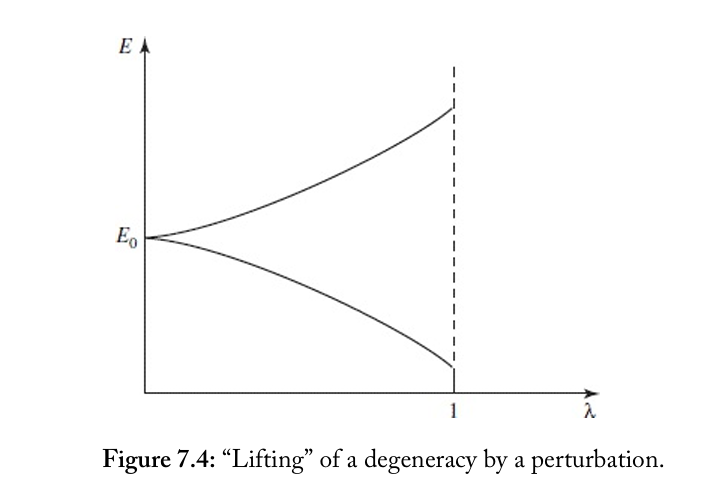
微扰后的退简并(图来源Introduction to Quantum Mechanics,3rd Edition--Griffiths | Figure 7.4)

现在做和与先前非简并态微扰相同的操作:

$E=E^{(0)}+ \lambda E^{(1)} + \lambda ^2 E^{(2)} + ... \qquad \psi =\psi ^{(0)} + \lambda \psi ^{(1)} + \lambda ^2 \psi ^{(2)} + ...$

同样代入定态薛定谔方程并合并 $\lambda$ 幂次相同的项:

$H_0 \psi ^{(0)} + \lambda (H^{'} \psi ^{(0)} +H_0 \psi ^{(1)} )+...=E^{(0)} \psi ^{(0)} + \lambda (E^{(0)} \psi ^{(1)}+ E^{(1)} \psi ^{(0)} )$

一阶近似

同样对于一阶情况 ( $\lambda ^1$ ) , 有

$H_0 \psi ^{(1)} + H^{'} \psi ^{(0)} = E^{(0)} \psi ^{(1)} + E^{(1)} \psi ^{(0)}$

使用 $\psi _a^{(0)}$ 与上式内积, 得:

$\langle \psi _a^{(0)} | H_0 \psi ^{(1)} \rangle + \langle \psi _a^{(0)} | H^{'} \psi ^{(0)} \rangle = E^{(0)} \langle \psi _a^{(0)} | \psi ^{(1)} \rangle + E^{(1)} \langle \psi _a^{(0)} | \psi ^{(0)} \rangle$

同样左一与右一相消, 再将 $\psi ^{(0)}=\alpha \psi _a^{(0)}+\beta \psi _b^{(0)}$ 代入上式并由正交归一可得:

$\alpha \langle \psi _a^{(0)} | H^{'} \psi _a^{(0)} \rangle + \beta \langle \psi _a^{(0)} | H^{'} \psi _b^{(0)} \rangle = \alpha E^{(1)}$

可紧凑的写为:

$\alpha H_{aa}^{'} + \beta H_{ab}^{'}=\alpha E^{(1)}$

刚刚是使用 $\psi _a^{(0)}$ 进行内积得到的结果, 现在再使用 $\psi _b^{(0)}$ 与一阶情况进行内积, 同理得

$\alpha H_{ba}^{'} + \beta H_{bb}^{'}=\beta E^{(1)}$

显然这是一个矩阵的形式, 而其元素正是 $H^{'}$ 对于无微扰的波函数 $\psi _a^{(0)}$ 和 $\psi _b^{(0)}$ 的矩阵元.即

$\begin{pmatrix}H_{aa}^{'} & H_{ab}^{'} \\ H_{ba}^{'} & H_{bb}^{'} \end{pmatrix} \begin{pmatrix}\alpha \\ \beta \end{pmatrix} =E^{(1)}\begin{pmatrix}\alpha \\ \beta \end{pmatrix}$

那么显然解其久期方程 (secular equation) 便可得到能量的一阶修正 $E^{(1)}$ 与系数 $\alpha$ , $\beta$ 的值, 由解出的系数便可得到由无微扰时的本征矢线性组合出来的 “好” 的零级近似态矢, 对于一阶近似态矢也是同理可推得

因此区别于非简并的一阶修正, 简并态的一阶修正是解微扰 $H^{'}$ 在简并子空间中的矩阵的久期方程, 即计算 $H^{'}$ 在简并的本征矢的表象下的矩阵元, 再计算其久期方程, 便可得到能量的一阶修正与 “好” 的近似出来的零级波函数.

二阶近似

同理继续可以推出简并态的二阶修正, 这里就不做推导了, 仅给出二级修正的矩阵元(简并态为简并于 $E_n$ 的 $n_1 , n_2 , n_3 , ... n_i , ... ,n_j ...$ ):

$G_{ij}=\sum_{m \ne n(all)}\frac{\langle n_i|H^{'}| m \rangle \langle m |H^{'}| n_j \rangle}{E_n^{(0)}-E_m^{(0)}}$

同理解由上述矩阵元组成的矩阵便可得到简并态的能量二阶修正, 这里不作赘述了.

含时微扰论

二能级系统

假设无微扰时系统只有 $\psi _a$ 与 $\psi _b$ 两个态, 且为无微扰哈密顿量 $H_0$ 的本征态:

$H_0 \psi _a =E_a \psi _a \qquad H_0 \psi _b =E_b \psi _b \qquad \langle \psi _a | \psi _b \rangle =\delta _{ab}$

由于其完备性, 任何状态都能表示为它们的线性组合, 并且系统的初态也可以表示为:

$\Psi (0)=c_a \psi _a + c_b \psi _b$

将时间演化算符 $U=e^{-iHt/ \hbar}$ 作用于初态则可以得到波函数随时间演化的情况

$\Psi (t)=c_a \psi _a e^{-iE_a t/ \hbar} + c_b \psi _b e^{-iE_b t/ \hbar}$

现假设引入一个含时微扰 $H^{'}(t)$ . 同理由于 $\psi _a$ 与 $\psi _b$ 的完备性, $\Psi (t)$ 仍可以表示为它们的线性组合, 唯一的区别是此时的系数 $c_a$ 与 $c_b$ 是时间 $t$ 的函数:

$\Psi (t)=c_a(t) \psi _a e^{-iE_a t/ \hbar} + c_b(t) \psi _b e^{-iE_b t/ \hbar}$

于是可以通过将上式代入含时薛定谔方程来求解 $c_a(t)$ 与 $c_b(t)$ , 即代入:

$H \Psi (t)=i \hbar \frac{\partial }{\partial t} \Psi (t) \qquad H=H_0+H^{'}(0)$

于是可得

$\begin{matrix}c_a(H_0 \psi _a )e^{-iE_a t/ \hbar}+c_b(H_0 \psi _b )e^{-iE_b t/ \hbar} +c_a(H^{'} \psi _a )e^{-iE_a t/ \hbar}+c_b(H^{'} \psi _b )e^{-iE_b t/ \hbar} \\ =i\hbar[\dot{c_a}\psi _a e^{-iE_a t/ \hbar} +\dot{c_b}\psi _b e^{-iE_b t/ \hbar} +c_a \psi _a (-\frac{iE_a}{\hbar})e^{-iE_a t/ \hbar}+c_b \psi _b (-\frac{iE_b}{\hbar})e^{-iE_b t/ \hbar}] \end{matrix}$

由定态薛定谔方程可将上式中的左式前两项与右式最后两项消掉, 即

$c_a(H^{'} \psi _a )e^{-iE_a t/ \hbar}+c_b(H^{'} \psi _b )e^{-iE_b t/ \hbar}=i\hbar(\dot{c_a}\psi _a e^{-iE_a t/ \hbar} +\dot{c_b}\psi _b e^{-iE_b t/ \hbar})$

为分离出 $\dot{c_a}$ ,使用 $\psi _a$ 与上式进行内积, 并由正交归一性得:

$c_a \langle \psi _a |H^{'}|\psi_a \rangle e^{-iE_a t/ \hbar} + c_b \langle \psi _a |H^{'}|\psi_b \rangle e^{-iE_b t/ \hbar}=i\hbar \dot{c_a}e^{-iE_a t/ \hbar}$

对其中的矩阵元进行缩写, 并两边同乘 $-(i/ \hbar)e^{iE_at/ \hbar}$ 则可得

$\dot{c_a}=-\frac{i}{\hbar}[c_a H_{aa}^{'}+c_b H_{ab}^{'}e^{-i(E_b-E_a)t/ \hbar}]$

同理使用 $\psi _b$ 进行内积则可分离出 $\dot{c_b}$ , 即:

$\dot{c_b}=-\frac{i}{\hbar}[c_a H_{bb}^{'}+c_b H_{ba}^{'}e^{i(E_b-E_a)t/ \hbar}]$

通常情况下 $H^{'}$ 的对角矩阵元为 $0$ , 证明过程见 Introduction to Quantum Mechanics,3rd Edition–Griffiths | Problem 11.5 . 要是本人不懒的话后面可能会在这里补起来证明过程. 因此方程可简化为:

$\dot{c_a}=-\frac{i}{\hbar}H_{ab}^{'}e^{-i\omega _0 t}c_b \qquad \dot{c_b}=-\frac{i}{\hbar}H_{ba}^{'}e^{i\omega _0 t}c_a$

其中(假定 $E_b \geqslant E_a$ , 即 $\omega _0 \geqslant 0$ )

$\omega _0=\frac{E_b - E_a}{\hbar}$

到目前为止的处理皆是严格, 对微扰大小未作任何假定. 而当 $H^{'}(t)$ 很小时, 则可以利用逐次近似法来求解 $\dot{c_a}$ 与 $\dot{c_b}$ 的方程. 设开始时粒子处于能量较低的状态, 即初态处于 $E_a$ 的概率为 $100%$ , 即:

$c_a(0)=1 \qquad c_b(0)=0$

零阶近似

即无微扰, 此时系统将继续保持这种状态

$c_a(t)=1 \qquad c_b(t)=0$

一阶近似

将零阶近似值代入上面求解 $\dot{c_a}$ 与 $\dot{c_b}$ 的方程, 可得

$\frac{dc_a^{(1)}}{dt}=0$

$\frac{dc_b^{(1)}}{dt}=-\frac{i}{\hbar}H_{ba}^{'}e^{i\omega _0 t}$

即:

$c_a^{(1)}(t)=1$

$c_b^{(1)}(t)=-\frac{i}{\hbar}\int _0^t H_{ba}^{'}(t^{'})e^{i\omega _0 t^{'}}dt^{'}$

二阶近似

同理将一阶近似值代入求解 $\dot{c_a}$ 与 $\dot{c_b}$ 的方程, 可得

$\frac{dc_a^{(2)}}{dt}=-\frac{i}{\hbar}H_{ab}^{'}e^{-i \omega _0 t}(-\frac{i}{\hbar})\int _0^t H_{ba}^{'}(t^{'})e^{i\omega _0 t^{'}}dt^{'}$

即

$c_a^{(2)}(t)=1-\frac{1}{\hbar ^2}\int _0^t H_{ab}^{'}(t^{'})e^{-i\omega _0 t^{'}}[\int _0^{t^{'}}H_{ba}^{'}(t^{''})e^{i \omega _0 t^{''}}dt^{'}]dt^{'}$

其它

原则上可以无限重复这套做法, 将 $n$ 阶近似代入到方程中, 求解 $n+1$ 阶的近似. 此外, 可将一阶近似的式子写成如下形式:

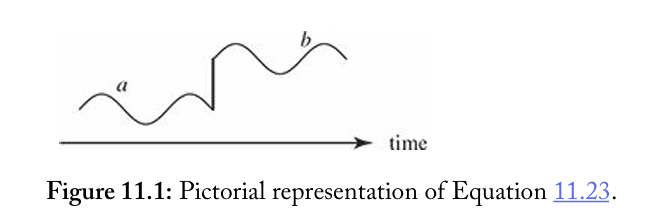
$c_b^{(1)}(t)e^{-iE_b t/ \hbar}=-\frac{i}{\hbar}\int _0^t e^{-iE_b (t-t^{'})/ \hbar}H_{ba}^{'}(t^{'})e^{-iE_a t^{'}/ \hbar}dt^{'}$

即还原了之前分离出的指数 $e^{-iE_b t/ \hbar}$ , 且此过程可用如下示意图解释, 即随着时间的演化, 从 $0$ 到 $t^{'}$ 系统处于 $\psi _a$ 态上, 其摆动来源于因子 $e^{-iE_a t^{'} / \hbar}$ ,并在 $t^{'}$ 时刻从 $\psi _a$ 态跃迁到 $\psi _b$ 态, 然后直到时间 $t$ 都保持在 $\psi _b$ 态上, 其摆动来源于因子 $e^{-iE_b(t-t^{'})/ \hbar}$ .当然此图仅作示例, 实际上这些状态并没有急剧的跃迁, 跃迁是发生在所有时间 $t^{'}$ 上

一阶近似下系统随时间演化的状态(图来源Introduction to Quantum Mechanics,3rd Edition--Griffiths | Figure 11.1)

在高阶和多能级系统中, 表达式将变得更为复杂, 以二阶近似为例, 式子可以同理写为如下形式:

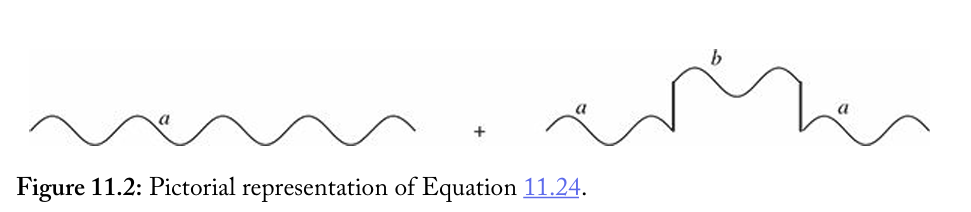
$\begin{matrix}c_a^{(2)}(t)e^{-iE_a t/ \hbar}=e^{-iE_a t/ \hbar}+(-\frac{i}{\hbar})^2 \int _0^t \int _0^{t^{'}} e^{-iE_a (t-t^{'})/ \hbar} \times \\ H_{ab}^{'}(t^{'})e^{-iE_b (t^{'}-t^{''})/ \hbar}H_{ba}^{'}(t^{''})e^{-iE_a t^{''}/ \hbar}dt^{''}dt^{'} \end{matrix}$

式中第一项是描述系统一直处于 $\psi _a$ 态上的第一个过程, 第二项是描述系统在时间 $t^{''}$ 从 $\psi _a$ 态跃迁到 $\psi _b$ 态, 然后在时间 $t^{'}$ 回到 $\psi _a$ 态的第二个过程, 即如图:

二阶近似下系统随时间演化的状态(图来源Introduction to Quantum Mechanics,3rd Edition--Griffiths | Figure 11.2)

于是还可以写出多能级系统的一般性结果:

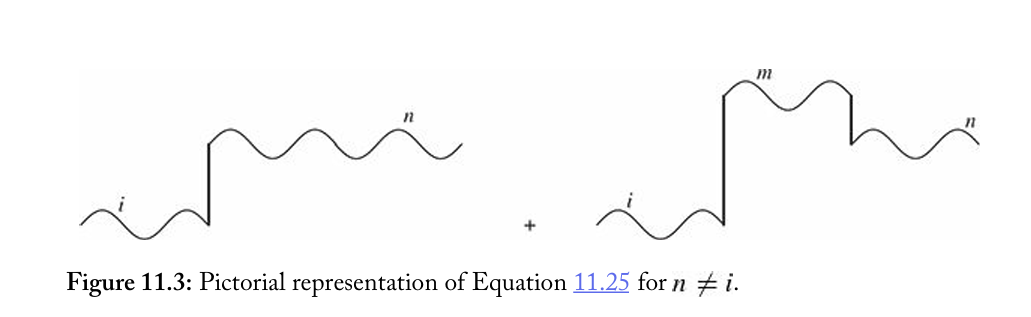
$\begin{matrix}c_n^{(2)}e^{-iE_n t/ \hbar}=\delta _{ni}e^{-iE_i t/ \hbar}+(-\frac{i}{\hbar})\int _0^t e^{-iE_n (t-t^{'})/ \hbar}H_{ni}^{'}(t^{'})e^{-iE_i t^{'}/ \hbar}dt^{'}+ \\ \sum _m (-\frac{i}{\hbar})^2 \int _0^t \int _0^{t^{'}}e^{-iE_n (t-t^{'})/ \hbar}H_{nm}^{'}(t^{'})e^{-iE_m (t^{'}-t^{''})/ \hbar}H_{mi}^{'}(t^{''})e^{-iE_i t^{''}/ \hbar}dt^{''}dt^{'} \end{matrix}$