最小作用量原理
如果一个力学体系的位形可以完全由一系列变量 q1,q2,...,qf 来唯一地描述 , 则称这一组变量为该力学体系的广义坐标 , 称 f 为该力学体系的自由度数目 , 对于这些变量并不一定是笛卡尔坐标 , 也可以是其它坐标形式 .
当然仅由广义坐标的数值并不能完全确定系统的"力学状态" , 因为此时所拥有的条件不足以预测下一时刻系统的位形 , 但如果知道这些广义坐标对于"时间"的微商 , 就可以完全确定任意时刻的位形了, 于是使用广义坐标 q 与其对时间的微商即广义速度 q˙ 就可以确定体系的状态并且预测以后的运动了 .
力学体系的运动规律可以通过最小作用量原理(哈密顿原理)给出 , 即力学体系具有一个与其运动相关的物理量 , 称为作用量 , 记作 S , 如果体系在给定的时刻 t1 和 t2 分别由给定的广义坐标 q1 和 q2 描写 , 那么该力学体系的作用量 S 可以表达为连接这两个位形之间的各种可能轨道的泛函 :
S=∫t1t2L(q,q˙,t)dt
其中函数 L(q,q˙,t) 称为体系的拉格朗日量 , 该力学体系在 t1 和 t2 之间连接广义坐标 q1 和 q2 的真实运动轨道就是使得作用量 S 取极小值的轨道
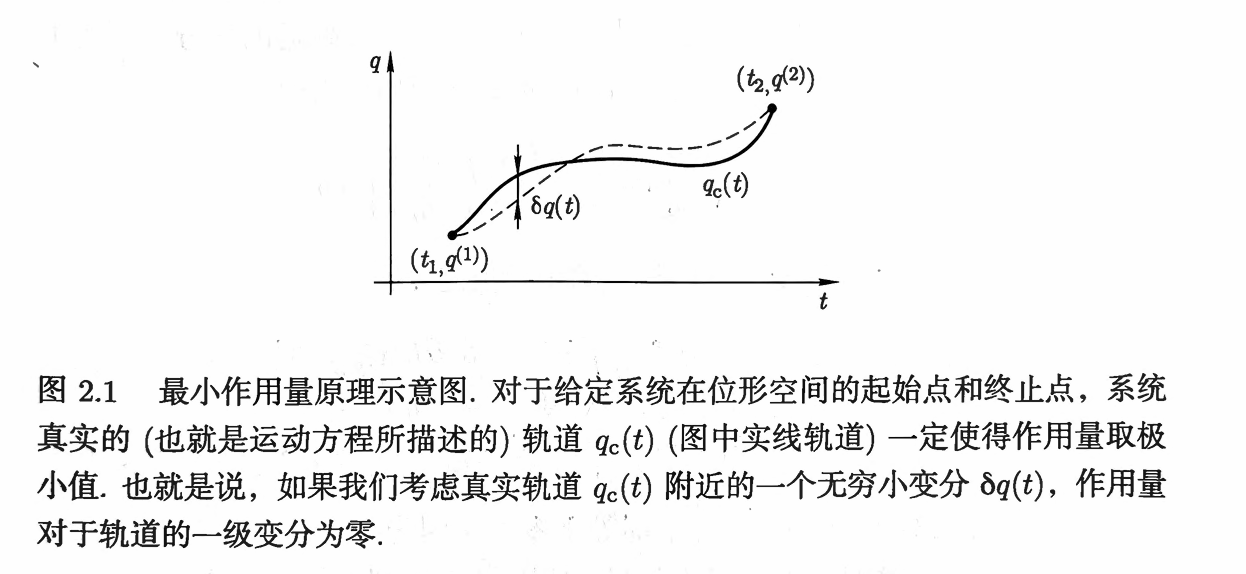
于是从最小作用量原理出发 , 利用变分法就可以求出力学体系的运动方程 , 即
δS=δ∫t1t2L(q,q˙,t)dt=0
欧拉-拉格朗日方程
由上述的论述可得 :
δS=∫t1t2[L(q+δq,q˙+δq˙)−L(q,q˙,t)]dt=∫t1t2(∂q∂Lδq+∂q˙∂Lδq˙)dt=∫t1t2[∂q∂Lδq+dtd(∂q˙∂Lδq)−dtd(∂q˙∂L)δq]dt=(∂q˙∂Lδq)∣t1t2+∫t1t2[∂q∂L−dtd(∂q˙∂L)]δqdt
由于初末时刻的广义坐标是确定的 , 显然 δq(t1)=δq(t2)=0 , 则上式中的第一项为零 , 又有最小作用量原理 δS=0 可得 :
δS=∫t1t2[∂q∂L−dtd(∂q˙∂L)]δqdt=0
于是有 :
dtd(∂q˙∂L)−∂q∂L=0
即欧拉-拉格朗日方程 .
对于有 f 个自由度的体系 , 则在最小作用量原理中有 f 个不同的函数 qi(t) 应该独立地变分 , 显然可以得到 f 个方程 :
dtd(∂qi˙∂L)−∂qi∂L=0(i=1,2,...,f)
能量守恒
由于时间具有均匀性 , 封闭系统的拉格朗日函数不显含时间 , 因此拉格朗日函数 L(q,q˙) 对时间的全导数可以写成 :
dtdL=i∑∂qi∂Lq˙+i∑∂qi˙∂Lqi¨
利用拉格朗日方程将 ∂qi∂L 替换为 dtd∂qi˙∂L , 得 :
dtdL=i∑qi˙dtd∂qi˙∂L+i∑∂qi˙∂Lqi¨=i∑dtd(∂qi˙∂Lqi˙)
整理可得 :
dtd(i∑∂qi˙∂Lqi˙−L)=0
由此可知
E=i∑∂qi˙∂Lqi˙−L
在封闭系统运动中保持不变 , 是运动积分 , 称为系统的能量 , 即封闭体系中的能量守恒 . 上述推导仅利用了拉格朗日函数不显含时间的性质 , 因此除了封闭系统以外 , 对于位于定常外场(即不显含时间)的系统也成立 .
由于封闭(或位于定常外场中的)体系的拉格朗日函数可以写成
L=T(q,q˙)−U(q)
或
L=a∑2mava2−U(r1,r2,...)
其中 T 是速度的二次函数 , 则
i∑∂qi˙∂Lqi˙=∂qi˙∂Tqi˙=2T
代入能量表达式则有
E=T(q,q˙)+U(q)
用笛卡尔坐标写成
E=a∑2mava2+U(r1,r2,...)
可见系统的能量可以表示为本质不同的两项之和 : 依赖于速度的动能和仅依赖于质点坐标的势能 .
动量守恒
根据空间均匀性 , 封闭力学体系在空间中整体平移时其性质保持不变 , 因此对于一个无穷小平移 ε 的变换 , 即 ra→ra+ε 在速度不变时 , 坐标的无穷小改变使拉格朗日函数产生的变化为
δL=a∑∂ra∂L⋅δra=ε⋅a∑∂ra∂L
由于 δL=0 , 则有
a∑∂ra∂L=0
由拉格朗日方程可得
a∑∂ra∂L=a∑dtd∂va∂L=dtda∑∂va∂L
即封闭力学体系的矢量
P=a∑∂va∂L
在运动中不随时间改变且为一常量 . 矢量 P 称为系统的动量 , 即封闭系统中力学体系的动量守恒 . 对拉格朗日函数 L=∑a2mava2−U(r1,r2,...) 求导可得到用质点速度表示的动量
P=a∑mava
如果用广义坐标 qi 描述运动 , 则拉格朗日函数对广义速度的导数
pi=∂qi˙∂L
称为广义动量 , 对广义坐标的导数
Fi=∂qi∂L
称为广义力 , 采用这种记号则可将拉格朗日方程写成
Fi=pi˙
角动量守恒
根据空间各向同性可得封闭体系整体在空间任意转动时其力学性质保持不变 , 因此对于一个无穷小转动矢量 δφ 有
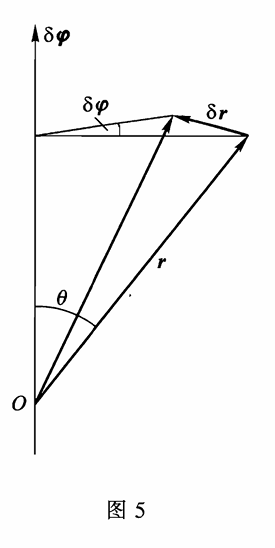
δr=δφ×r
δv=δφ×v
带入转动时拉格朗日函数不变的条件
δL=a∑(∂ra∂L⋅δra+∂va∂L⋅δva)=0
并做代换 ∂va∂L=pa , ∂ra∂L=pa˙ , 得
a∑[pa˙⋅(δφ×ra)+pa⋅(δφ×va)]=0
即
δφ⋅a∑(ra×pa˙+va×pa)=δφ⋅dtda∑ra×pa=0
由 δφ 的任意性可得
dtda∑ra×pa=0
即在封闭力学体系运动过程中矢量
M=a∑ra×pa
不随时间改变 , 这个矢量称为系统的角动量 , 即封闭体系的角动量守恒 .
[等待更新]
最近几天爽玩机战Y , 好爽好爽



