银河旋臂测绘原理

文章目录

1. 1. 银河系旋臂与中性氢
2. 2. 21cm/1420MHz 谱线
3. 3. 绘制旋臂的几何原理

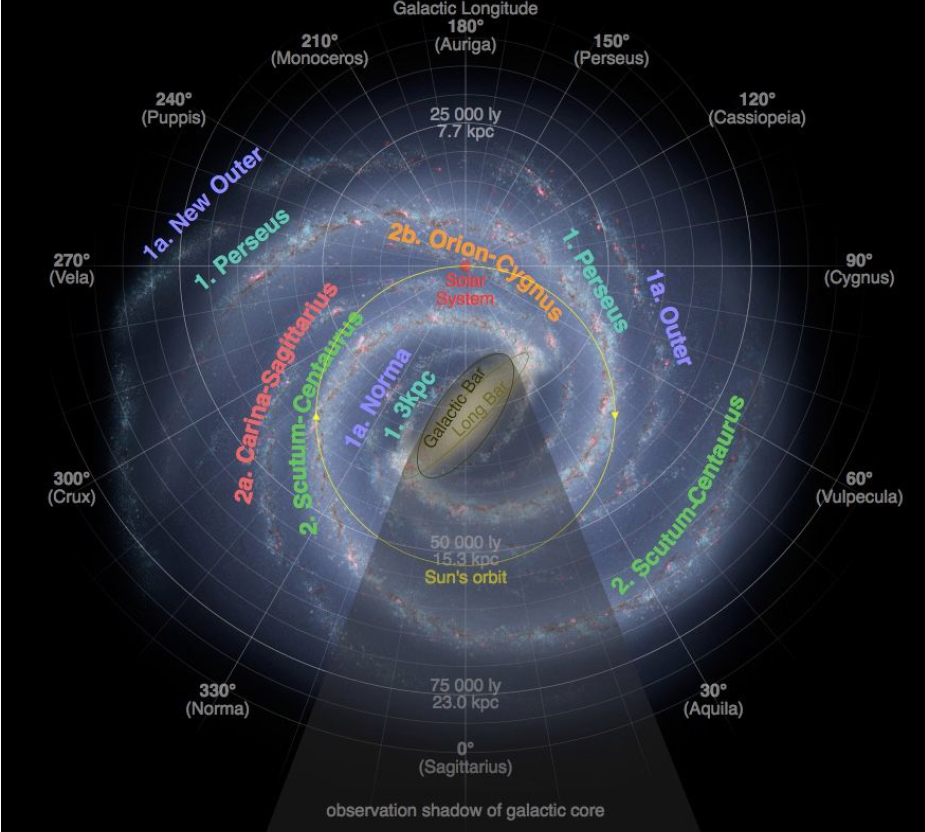
银河系旋臂与中性氢

 根据当前的标准宇宙大爆炸模型预测, 在原初的大爆炸核合成过程中, 首先是由质子与中子合成了氢、氦及极少量锂, 使早期宇宙中的可见物质含有约75%的氢(主要是质子)、约25%的氦(主要是 $^4He$ )和极少量的锂(几乎都是 $^7Li$ ). 此后再由许多过程演化出现在宇宙的其它元素.

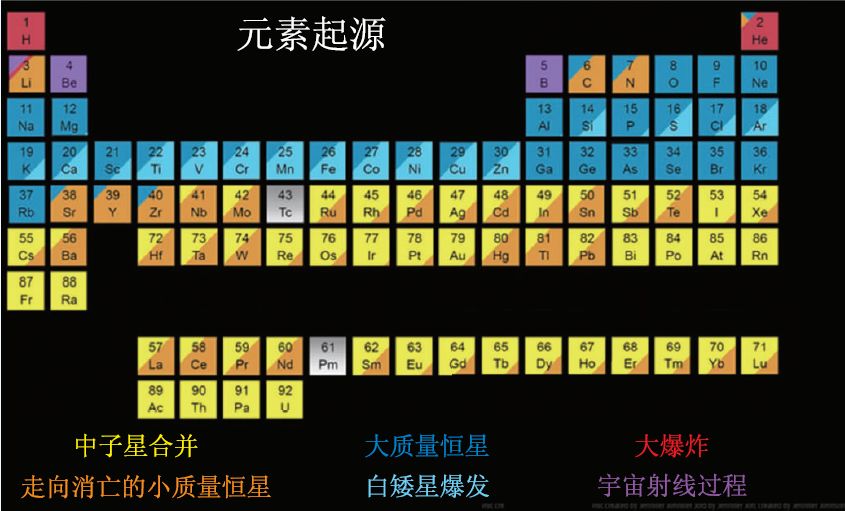
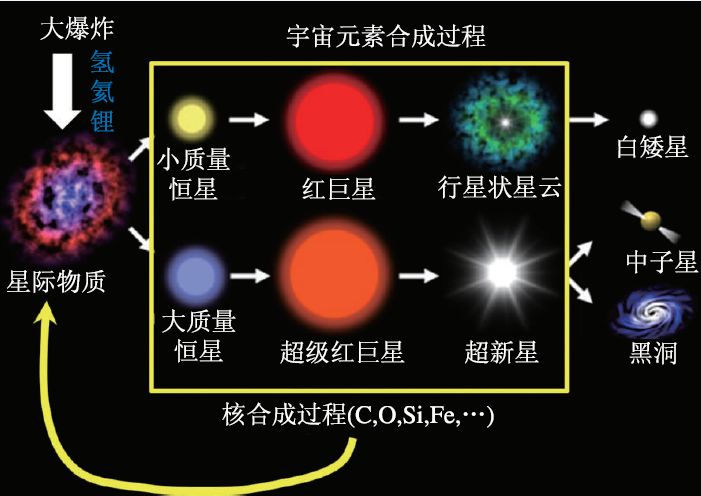
因此在银河系当中, 氢的丰度是最高的, 尤其在银河旋臂处含有大量的中性氢, 而天然氢原子由一个质子和一个环绕质子的电子组成, 且二者均有自旋, 而由于 自旋平行 与 自旋反平行 的能量不同, 所以在这两种不同的态间跃迁时则会辐射出电磁波, 也就是 21cm氢谱线 .下面将介绍这一频率的谱线.

21cm/1420MHz 谱线

 质子与电子的磁矩分别为:

$\boldsymbol{\mu}_p=\frac{g_p e}{2m_p}\boldsymbol{S}_p \qquad \boldsymbol{\mu}_e=-\frac{e}{m_e}\boldsymbol{S}_e$

不过质子的磁偶极子要比电子小很多. 又由经典电动力学(详见D.J.Griffiths,Am.J.Phys.,50,698(1982).)可知, 一个磁偶极子形成的磁场为:

$\boldsymbol{B}=\frac{\mu_0}{4\pi r^3}[3(\boldsymbol{\mu}\cdot \hat{r})\hat{r}-\boldsymbol{\mu}]+\frac{2\mu_0}{3}\boldsymbol{\mu}\delta^3(\boldsymbol{r})$

由 $H=-\boldsymbol{\mu}\cdot \boldsymbol{B}$ 可得位于质子磁偶极矩形成的磁场中的哈密顿量为:

$H_{hf}^{'}=\frac{\mu_0 g_p e^2}{8\pi m_p m_e}\frac{[3(\boldsymbol{S}_p \cdot \hat{r})(\boldsymbol{S}_e \cdot \hat{r})-\boldsymbol{S}_p \cdot\boldsymbol{S}_e]}{r^3}+\frac{\mu_0 g_p e^2}{3 m_p m_e}\boldsymbol{S}_p \cdot \boldsymbol{S}_e \delta^3(\boldsymbol{r})$

于是由微扰理论, 可得能量的一级修正( $E^{1}=\langle \psi | H^{’} | \psi \rangle $ )为:

$E_{hf}^{1}=\frac{\mu_0 g_p e^2}{8\pi m_p m_e} \langle \frac{[3(\boldsymbol{S}_p \cdot \hat{r})(\boldsymbol{S}_e \cdot \hat{r})-\boldsymbol{S}_p \cdot\boldsymbol{S}_e]}{r^3} \rangle +\frac{\mu_0 g_p e^2}{3 m_p m_e} \langle \boldsymbol{S}_p \cdot \boldsymbol{S}_e \rangle |\psi(0)|^2$

对于基态或l=0的其它态而言波函数是球对称的, 因此式中第一项的平均值为0, 又由于氢原子基态 $\psi_{100}=\frac{1}{\sqrt{\pi a^3} }e^{-r/q}$ ,则可得 $|\psi_{100}(0)|^2=\frac{1}{\pi a^3 }$ ,则对于基态有:

$E_{hf}^{1}=\frac{\mu_0 g_p e^2}{3 \pi m_p m_e a^3} \langle \boldsymbol{S}_p \cdot \boldsymbol{S}_e \rangle$

它被称为自旋–自旋耦合, 而对于这种耦合方式, 同样取总自旋的本征矢作为好的量子态, 即取

$\boldsymbol{S}=\boldsymbol{S}_e+\boldsymbol{S}_p$

的本征矢作为量子态. 将该式平方则可以得到:

$\boldsymbol{S}_p \cdot \boldsymbol{S}_e=\frac{1}{2}(S^2-S_e^2-S_p^2)$

由于电子质子都具有 $\frac{1}{2}$ 自旋, 因此 $\frac{1}{2} \oplus \frac{1}{2}$ 耦合后的总自旋为1与0. 即对于三重态, 其总自旋为1

$S_e^2=S_p^2=\frac{1}{2}(\frac{1}{2}+1)\hbar^2=\frac{3}{4}\hbar^2$

$S^2=1x(1+1)\hbar^2=2\hbar^2$

对于自旋单态, 其总自旋为0, 同样

$S_e^2=S_p^2=\frac{1}{2}(\frac{1}{2}+1)\hbar^2=\frac{3}{4}\hbar^2$

$S^2=0x(0+1)\hbar^2=0$

因此

$E_{hf}^1=\frac{4g_p\hbar^4}{3m_pm_ec^2a^4}\begin{cases}+1/4, & \text{三重态} \\-3/4, & \text{单态} & \end{cases}$

即自旋–自旋耦合打破了基态的自旋简并, 抬高了三重态的能级, 降低了单态的能级

二者之间的能级间隔为:

$E_{hf}^1=\frac{4g_p\hbar^4}{3m_pm_ec^2a^4}=5.88x10^{-6}eV$

于是从三重态跃迁到基态所释放的光子频率与波长为:

$\nu=\frac{\Delta E}{h}=1420MHz$

$\lambda=\frac{c}{\nu}=21cm$

也就是大名鼎鼎的 $21cm$ 氢谱线 . 于是便可以通过天线来接受位于 $21cm$ 波段的电磁波来判断中性氢的存在.

绘制旋臂的几何原理

 由多普勒效应

$\frac{\Delta f}{f_0}=\frac{V_r}{c}$

其中 $\Delta f=f-f_0$ 为观测谱线的频移, $f_0$ 为氢谱线的固有频率 $1420Mhz$ , $V_r$ 为中性氢相对于观测者的径向速度, $c$ 为光速. 因此基于多普勒效应可以计算出氢分子云在地球参考系中的径向速度 $V_r^{'}$ ,此外利用Python的astropy天文包可以将在地球参考系的径向速度 $V_r^{'}$ 修改为日心参考系的径向速度 $V_r$ ,即消除地球自转与公转的影响. 接下来讨论旋臂结构的绘制.

 当观察位于银道面不同经度的氢分子云时, 其径向速度为

$V_r=V\cdot cos \alpha -V_0 \cdot sin c$

其中 $V$ 是氢分子云的速度, $V_0$ 是太阳绕银心的速度. 该方程还可以简化为:

$V_r=V \frac{R_0}{R}sin l -V_0 sin l$

其中 $R_0$ 是太阳与银心的距离, $R$ 是氢分子云与银心的距离，$l$ 是氢分子云的银经. 假设星系中的元素服从差动自转, 这意味着圆周速度与半径成常数，即 $V_r=V_0$ ,则可得到:

$R=\frac{R_0 V_0 sin l}{V_0 sin l +V_0}$

若假设 $R_0=8.5kpc$ , $V_0=220km/s$ ,再由前面的频谱信息所得到的径向速度 $V_r$ 则可计算出不同经度 $l$ 下氢分子云与银心的距离 $R$ . 同时在三角形CSM中使用余弦定理可得

$R^2=R_0^2+r^2 -2R_0 \cdot r \cdot cosl$

其中 $r$ 为氢分子云到太阳的距离. 于是可得

$r_{\pm}=\pm \sqrt{R^2-R_0^2 sin^2 l}+R_0 cos l$

在这个方程中, 可得到两个不同的值, 只取单个正值，然后使用以下公式计算笛卡尔坐标的值：

$x=rcos(l-90°)$

$y=rsin(l-90°)$

于是通过计算不同经度下不同速度的 $x$ 与 $y$ 值,并将其绘制出来,便可以得到银河的旋臂结构.

有点想摸鱼了,后面的等以后再更新吧

---

参考:

1. 宇宙中元素的起源

2. The Rotation Curve and Spiral Structure of Milky Way from the Hydrogen 21-cm Line Detection with Campus Radio Telescope

3. MilkyWay

---

等待更新…